大顶堆小顶堆与堆排序
一直对堆排序算法用的不错,但是又是在排序中挺重要的算法,并且可以求解其他问题,比如top k问题。已经对堆排序学习过好多次了,无奈每次都记不太清楚具体的细节问题,本文对堆的问题进行整理。本文的排序例子来源于严蔚敏的《数据结构》,本文的知识点来自《算法导论》。
最大堆为堆中的最大元素位于根节点,顾名思义,最小堆的根节点为最小值。堆的性质决定了堆中节点一定大于等于其子节点。在堆排序算法中用到的是最大堆,最小堆用于构造优先队列,要是使用最小堆进行排序,得到的排序结果为倒序。
堆的结构为完全二叉树,因此可以用数组存储来代替树的链式存储结构。
建最大堆过程
我这里通过图表的形式对建大顶堆的过程进行了展示,不再对文字进行叙述。在堆排序的过程中会不断进行建最大堆过程的调用。
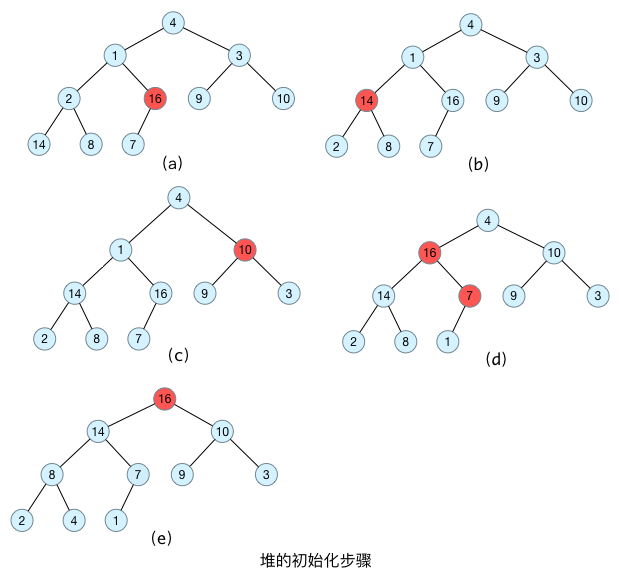
堆排序的核心步骤
清楚了堆的初始化,再看一下下面的堆排序步骤就非常清楚了,不需要图片进行描述了。堆排序的步骤:
- 将待排序的数组初始化为大顶堆,该过程即建堆。
- 将堆顶元素与最后一个元素进行交换,除去最后一个元素外可以组建为一个新的大顶堆。
- 新建立的堆不是大顶堆,需要重新建立大顶堆。重复上面的处理流程,直到堆中仅剩下一个元素。
top k问题的堆解法
该问题最常规和通用的解决思路为使用快速排序,还可以在N的范围不大的情况下采用哈希(桶)的方式。
另外一种解法就是堆排序的思路来解决。这里用到的为最小堆,用最小堆来存储最大的k个数,其中堆顶元素为最大k个数种最小的数。这个解法初看有些别扭,求最大的k个数,居然会用到小顶堆。
该算法必然是一个个遍历N个数一次就够了,这点很好理解。每读取一个新的数x,如果x比堆顶的元素y小,则抛弃;如果x比y大,则用x替换y,并重新更新堆。